
Restar fracciones es quitar una parte de otra. Imagina que tienes 3/4 de una pizza y comes 1/4: ¿cuánto queda? Esa es la esencia de esta operación, donde sustraes una fracción para saber cuánto queda del total.
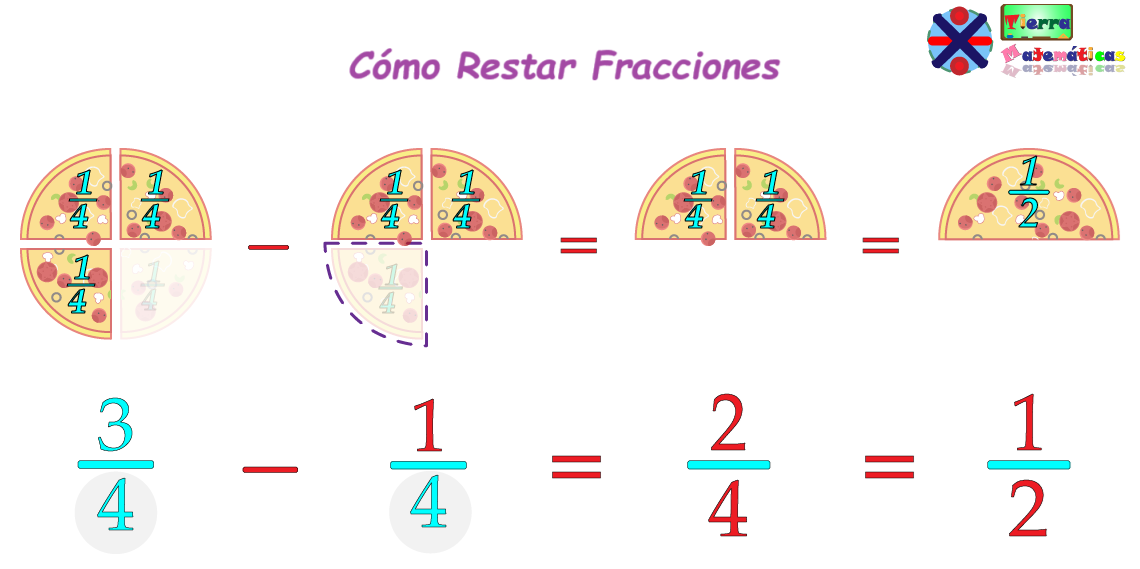
Para que la resta funcione, primero necesitamos asegurarnos de que las fracciones tengan el mismo denominador, o un denominador común. Y aquí es donde entra en juego el denominador común.
Un denominador común es el número que los denominadores (los números de abajo) de las fracciones tienen en común. Por ejemplo..., ¾ - ¼.
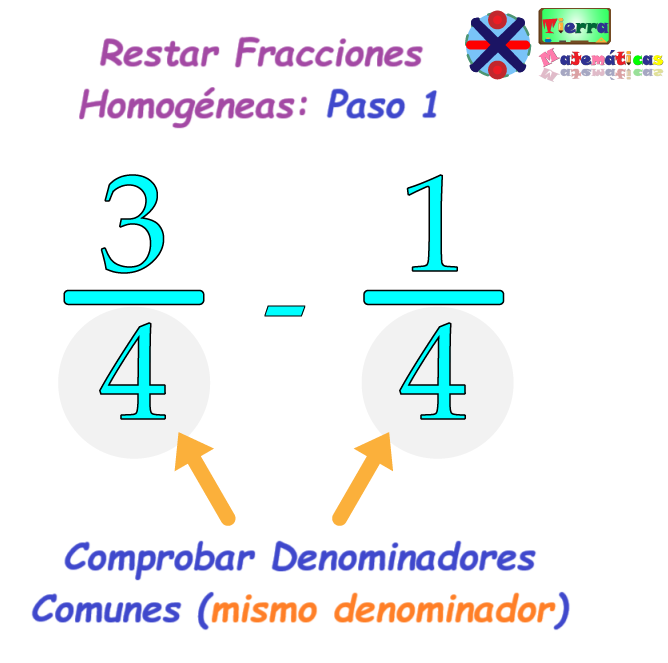
Al ser homogéneas, ambas fracciones tienen el mismo denominador, podemos simplemente restar los numeradores (los números de arriba) y mantener los denominadores iguales.
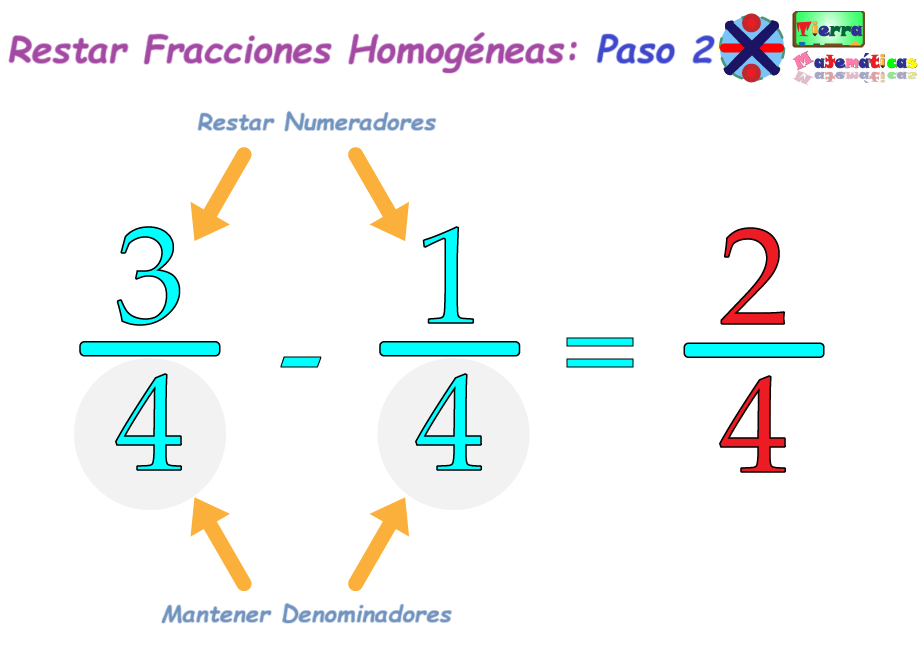
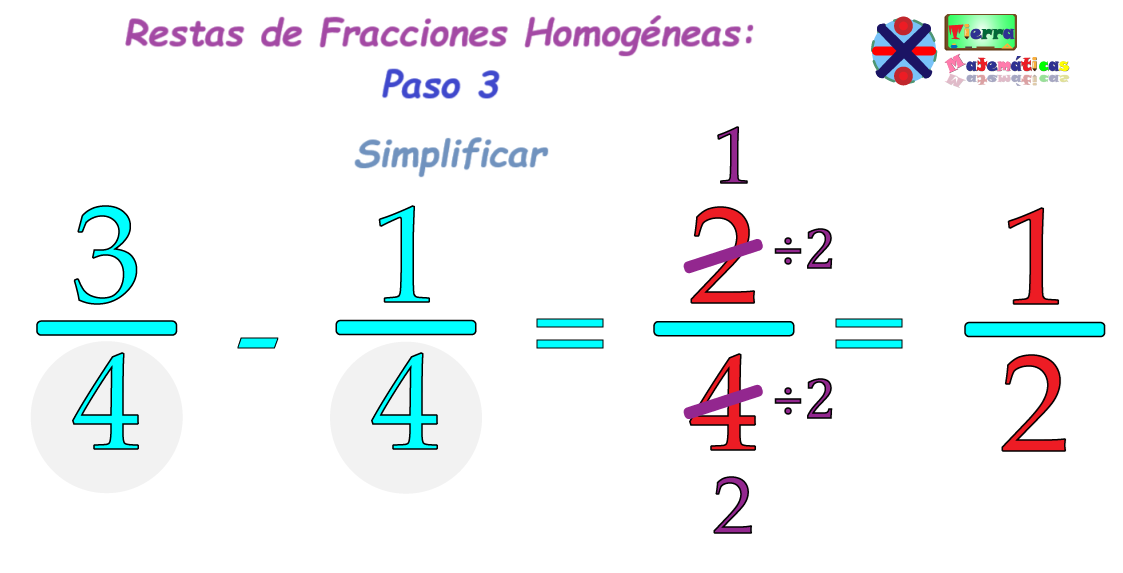
Para simplificar una fracción, necesitamos encontrar el número más alto que pueda dividir tanto el numerador como el denominador sin dejar sobrante. A este número se le llama Máximo Común Divisor (MCD).
Ejemplo: El resultado de la resta es la fracción 2/4.
- Divisores de 2: 1, 2
- Divisores de 4: 1, 2, 4
El mayor divisor en común es 2, por lo tanto:
Resultado final: La fracción 2/4 se simplifica a 1/2.
Fracciones heterogéneas son fracciones con denominadores diferentes. En otras palabras, los números que se encuentran en la parte inferior son distintos.
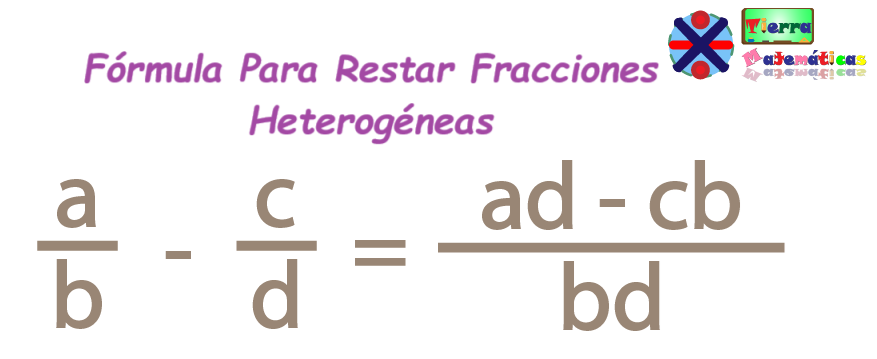

Si los denominadores son distintos, lo primero que debemos hacer al restar fracciones es encontrar un denominador común.
Lograremos hallar ese denominador común usando el mínimo común múltiplo (MCM) de los denominadores.
El MCM es el número más pequeño que ambos denominadores pueden usar para dividir de manera exacta, sin dejar ningún residuo. ¡Aprendamos cómo encontrarlo!
Para encontrar el MCM fácilmente, necesitamos listar los múltiplos de cada denominador — en este caso, los múltiplos de 2 y 5. Luego, identificamos los múltiplos que ambos números tienen en común.
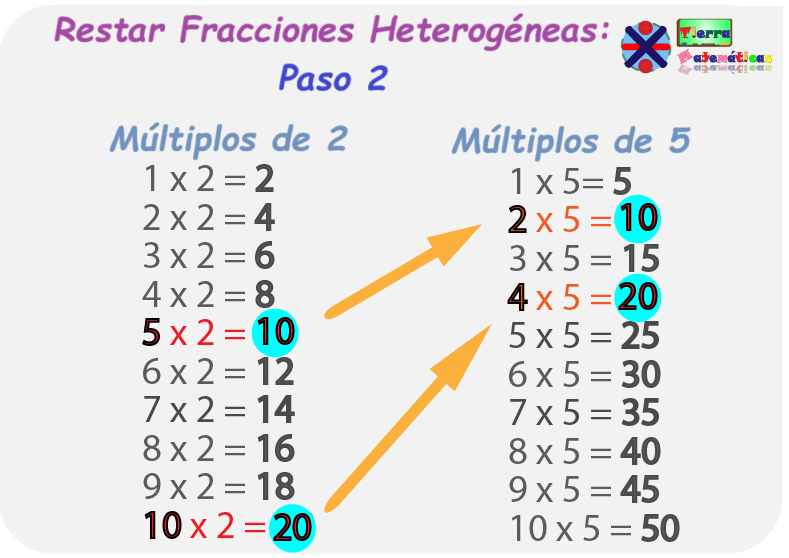
Hemos identificado los múltiplos que ambos números comparten:
Múltiplos de 2
10, 20, etc.
Multiplos de 5
10, 20, etc.
Después de listar los múltiplos que 2 y 5 tienen en común, vemos que el número más pequeño que está presente en las dos listas es el 10, así que 10 será el MCM.

Después de obtener el MCM, que es 10, necesitamos convertir las dos fracciones para que compartan el mismo denominador.
En este caso, para igualar los denominadores, multiplicamos el primer denominador (2) por 5 para obtener el MCM, que es 10. Luego, multiplicamos el segundo denominador (5) por 2 para llegar también a ese mismo MCM (10).
Luego, ajustamos los numeradores en proporción al cambio de denominador. Si el denominador fue multiplicado por 5 para alcanzar el MCM, entonces el numerador también debe multiplicarse por 5, continuando el proceso también con la siguiente fracción, pero esta vez usando el 2.
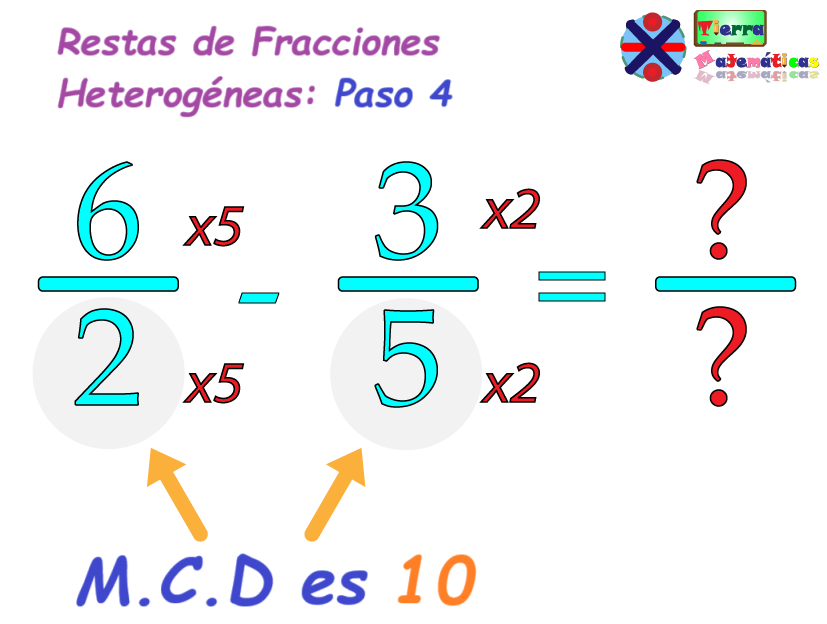
Después de multiplicar ambos denominadores para obtener el MCM y los numeradores para hacer las fracciones equivalentes, podemos reescribir las fracciones con los nuevos numeradores y denominador.
Luego, resolvemos la fracción restando los numeradores y manteniendo el denominador común.
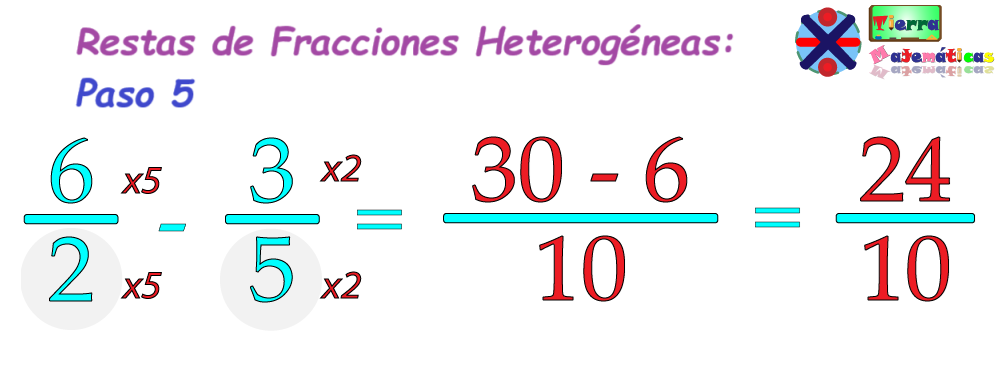
Una vez restadas las fracciones, conviene revisar si el resultado puede reducirse. Esto lo hacemos dividiendo el numerador y el denominador por su mayor divisor común. Por ejemplo, en la fracción 24/10, ambos pueden dividirse entre 1 y 2.
En este caso, entre estos números, 2 es el de mayor valor, por lo cual elegimos
2 como el MCD y procedemos a dividir el numerador y el denominador por 2.
Al momento de dividir al numerador y denominador por 2, obtenemos 12/5.

