La sustracción o resta básicamente significa retirar cosas de algo, especialmente números, es una de las operaciones aritméticas básicas y es usada para calcular el resultado o la diferencia entre dos cosas contables o números.
La sustracción ayuda en cada cosa que hagamos en la vida, como contar cuántos artículos te quedan después de regalar algunos.
Debajo hay algunos ejemplos para que entiendas más sobre el proceso de sustracción.
Esta representación visual puede mejorar el entendimiento de sustraer. Aquí puedes visualizar el concepto:
Una recta numérica es una de las formas más sencillas e intuitivas de visualizar el concepto de sustracción.

Recuerda la idea básica de sustracción.
- Imagina un conjunto de 5 manzanas:

- Te comes 2 de ellas

- Luego te deshaces de las manzanas que te comiste
- Después de eliminar las manzanas comidas. ¿Cuántas manzanas te quedan?

- Entonces, 5 - 2 = 3 😊
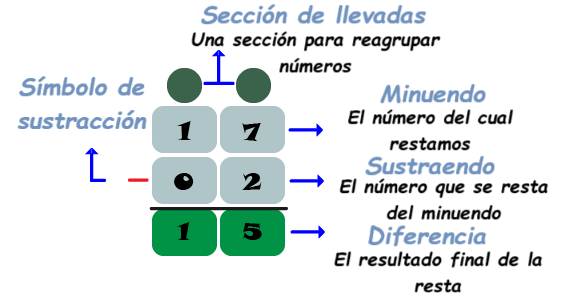
Las partes de la resta son principalmente 3 (minuendo, sustraendo y diferencia), pero también podemos identificar el signo de la resta y la *sección de llevadas.
El número del cuál restamos
El número que se resta del minuendo
El resultado final de la resta
Aunque esta sección no es una parte formal de la resta, es útil considerarla dentro del proceso para ayudar a los niños a entender la resta de una manera más fácil.
El signo que representa el proceso de restar.
La resta con reagrupación se utiliza cuando restamos números usando el método vertical y encontramos que un dígito en el sustraendo (el número que se está restando) es mayor que el dígito correspondiente en el minuendo (el número del que estamos restando). En este caso, necesitamos reagrupar o pedir prestado de la columna siguiente a la izquierda. Esto implica tomar 1 de esa columna, reducirla en 1 y agregar 10 a la columna actual para hacer posible la resta.
Debes repetir el proceso para cada columna hasta que hayas completado el proceso de resta.
Con nuestra pizarra de restas puedes visualizar el proceso de la reagrupación fácilmente como se muestra en los siguientes ejemplos
1) Primero, identificamos que ' 7 ' is más que ' 5 '.
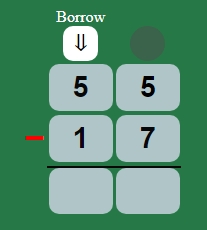
2) Así que, prestamos un grupo de ' 10 ' de la siguiente columna, eso signifíca que en teoría ya no sería ' 55 ', y ahora sería ' 45 '.

3) Ahora que hemos prestado ' 10 ', agregamos ' 5 + 10 ', y se convierte, como se ve en la ilustración, en ' 15 '.
Después debemos encontrar un número que agregado a ' 7 ' es igual a ' 15 '.

4) Y finalmente ..

Y eso es restar usando la reagrupación! 😊
Consejos para Maestros y Padres
El uso de ayudas visuales como rectas numéricas, modelos de conjuntos y otros métodos puede mejorar significativamente la comprensión del proceso de la resta. Permiten a los estudiantes o aprendices ver el proceso de restar, haciendo que el concepto abstracto sea más accesible. Este enfoque multimodal fomenta una comprensión más profunda de la resta, tanto como operación numérica como concepto aplicado en la vida real.